In my earlier series about the Buddhabrot I vilely slandered Brent’s Cycle Detection Algorithm as “kind of a dud.” Well, I’m 99% sure I implemented it wrong the first time I tried it out (oops) so I think it’s time to give it a fairer shot.

I came across the concept of an automatic iteration limit algorithm for finding out whether a point is inside the Mandelbrot set. In this method, there isn’t an explicit maximum iteration count passed in - it will only stop iterating if the point escapes or it detects a cycle. The cycle detection algorithm better work in this case!

Finite Iteration Limit

Here’s a simplfied traditional version of the finding out whether a point is inside the Mandelbrot set:

public bool IsPointInMandelbrotSet(Complex c, int maxLimit)
{
    var z = Complex.Zero;

    for (int i = 0; i < maxLimit; i++)
    {
        z = z * z + c;

        // check if the point has escaped the circle of radius 2
        if (z.Magnitude > 2)
        {
            return false;
        }
    }

    // Point never escaped, so we think it's in the Mandelbrot set
    return true;
}

If we feed this method a complex number inside the set, it will take exactly maxLimit iterations to return.

Automatic Iteration Limit

Let’s see it without the max limit parameter:

public bool IsPointInMandelbrotSet(Complex c)
{
    var z = Complex.Zero;
    var oldZ = Complex.Zero;

    int stepsTaken = 0;
    int stepLimit = 2;

    int iterations = 0;

    while (z.Magnitude <= 2)
    {
        z = z * z + c;

        // z matches an old value, so we found a cycle
        if (z == oldZ)
            return true;

        // Time to update the old value
        if (stepsTaken == stepLimit)
        {
            oldZ = z;
            stepsTaken = 0;
            stepLimit *= 2;
        }

        stepsTaken++;
        iterations++;
    }

    // Point escaped, so it's not in the Mandelbrot set
    return false;
}

For points inside of the set, it relies entirely on the cycle detection algorithm for knowing when to stop.

When I implemented it the first time, I screwed up when the values were compared (basically, the z == oldZ part was inside the next if statement). I also didn’t use a separate counter for stepsTaken either, which I’m sure screws up the math. In my defense, the pseudo code on Wikipedia is a bit unclear and isn’t exactly the same usecase as this.

Is it fast?

Well, it depends on your max iteration limit and the points you’re feeding it… If you have a really low iteration limit, it might take substantially more iterations to find a cycle than just iterating for a set amount.

Let’s benchmark this. We’ll compute a 25x25 grid of points in a complex area with real bounds of (-1.45, 0.75) and imaginary bounds of (-1.1, 1.1). This will give us a good mix of points outside and inside the set. We’ll leave out threading and geometric checks that can short-circuit the algorithm and plot the relative speed of each method (using the finite limit approach as the baseline; I.E. 1).

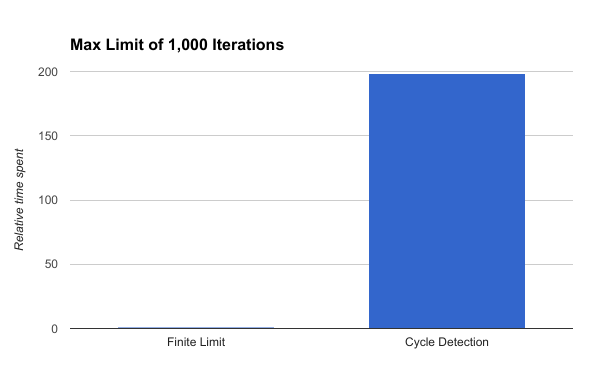
Yowza. The cycle detection method is nearly 200x slower!

Let’s see what happens when we bump up the iteration limit to 1 million:

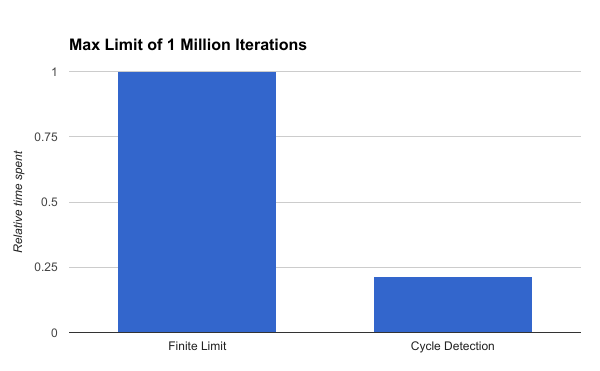
That’s better - the cycle detection is able to bail out of the loop far earlier than 1 million iterations.

Best of Both Worlds?

Of course, there’s nothing preventing us from combining both approaches:

public bool IsPointInMandelbrotSet(Complex c, int maxLimit)
{
    var z = Complex.Zero;
    var oldZ = Complex.Zero;

    int stepsTaken = 0;
    int stepLimit = 2;

    for (int i = 0; i < maxLimit; i++)
    {
        z = z * z + c;

        if (z.Magnitude > 2)
        {
            return false;
        }

        if (z == oldZ)
            return true;

        if (stepsTaken == stepLimit)
        {
            oldZ = z;
            stepsTaken = 0;
            stepLimit *= 2;
        }

        stepsTaken++;
    }

    return true;
}

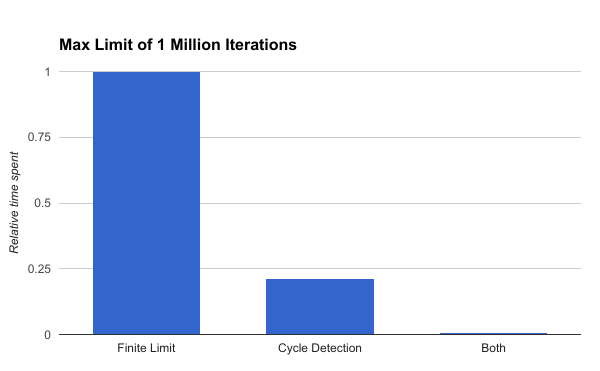
The results are better in both cases:

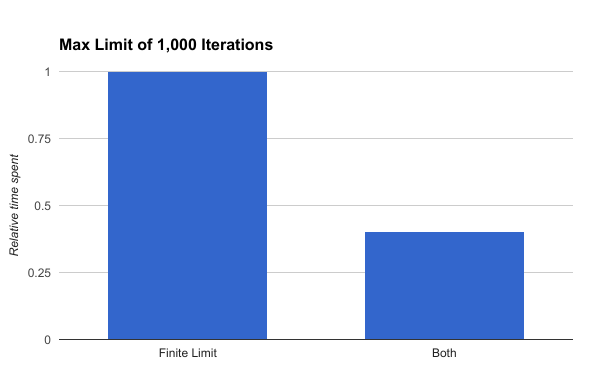(I left out the cycle-detection only method because it was so amazingly bad in this benchmark)

Conclusion

Well, I think the results speak for themselves. Brent’s Cycle Detection Algorithm is a great thing to use when doing Mandlebrot set calculations, especially once you start getting into massive iteration limits. Its honor has been restored.