At the inaugural Indy.Code() conference I presented on how I generated a 68.7 gigapixel rendering of the Buddhabrot fractal. For now, all you need to know is that it’s this thing…

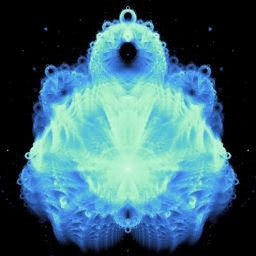
…but really, really gigantic.

In this series I’ll explain what the Buddhabrot is and how I made my version.

Series Overview

• Part 1 - What is the Mandelbrot set?
• Part 2 - What is the Buddhabrot?
• Part 3 - Algorithmic Optimizations
• Part 4 - Code Optimizations
• Part 5 - The Big Reveal

Introduction

I was introduced to the Buddhabrot in a college class about fractals (technically, it was about Chaotic Dynamical Systems but I don’t remember too much about that). A few years ago at SEP we introduced Hackathon Weekends. The Buddhabrot seemed like the perfect topic for a weekend project so we (I managed to convince two others to help) set out to render a 500 megapixel version. This was heavily inspired by Johann Korndoerfer’s 500 megapixel version he made in LISP. I decided to use C#/.NET because that’s what I’m most comfortable with.

We succeeded! Although impressive, I was a bit unsatisfied with all the shortcuts we had to take to accomplish anything in a weekend. I decided to revisit it in a second Hackathon and raised it to 625 megapixels. That might seem like a modest increase, but the 500 megapixels was a hard limit with the original method. (As it turns out, the .NET Image class will throw an undocumented Win32 exception if you try to create an image larger than 500MP. Geez, don’t they test anything over there at Microsoft?!!!)

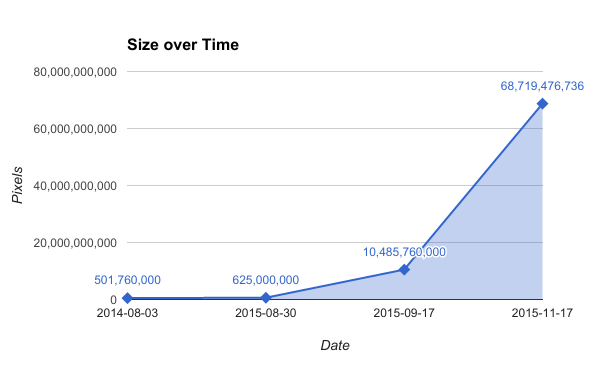
At this point I was hooked so I pushed it up to 10 gigapixels. I immediately realized my mistake and pushed it to the largest possible version I could create without radically altering my approach - 68.7 gigapixels!

Aside - 68.7 gigapixels? What a weird number

Now, the number 68.7 might jump out at you because it doesn’t sound very computer-sciencey. How you refer to the size depends on whether you consider a kilopixel to be 1,000 or 1,024 pixels. If you go by 1,024, the size is actually 64 gigapixels. Since the only people who actually care about megapixels are camera manufacturers (and they cheat as much as they can get away with) I’ll go for the more impressive number.

In unambiguous terms, the final rendering is 68,719,476,736 pixels (262,144 by 262,144).

What is a Fractal?

A fractal is defined by self similarity - parts of the object are similar to the whole.

A classic example of a fractal that you may have seen is the Sierpinski Triangle:

Fractals have sometimes been described as “the mathematics of nature” because this concept often shows up in the real world. Take the example below:

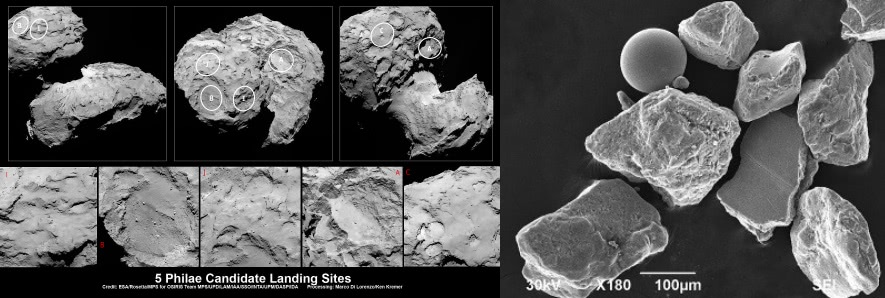
On the left, we have the comet that the Rosetta spacecraft landed on in 2014. On the right, grains of dust under extreme magnification. Even though the scales are wildly different they look pretty similar!

Fractals do have real-world applications, but the one we’ll be looking at in this series doesn’t do too much other than look cool.

What is the Mandelbrot Set?

The Mandelbrot set has been called “the king of fractals.” We’ll have to use a bit of math to explain what it is, but don’t worry, there won’t be any scary theoretical stuff.

Complex Numbers

The most complicated mathematical concept we have to introduce is complex numbers. A complex number is written as a + bi where a is a real number and b is an imaginary number (remember that i is the square root of negative one).

Just like “normal” numbers, you can add and multiply complex numbers. These rules are very straightforward, but you can look those up yourself if you are interested. The important thing to keep in mind is that a complex number has two independent components and that addition/multiplication isn’t quite the same as a normal number.

The Complex Plane

Since complex numbers have two different parts we can draw one in two dimensions. Mathematicians display them on something called the complex plane:

Here we’re looking at a circle of radius 2 around the origin (yes, the value of 2 is special, but we’re not going to go into why). The real numbers go across the X-axis and the imaginary numbers are on the Y-axis. See the white dot? That’s -1 + 0.25i, as an example.

The Magic Function

Let’s introduce a function:

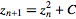
where z and c are both complex numbers. We’ll pick any starting point within the gray circle of radius 2 and call it c. Starting with z = 0, the function says that to calculate the next z value, we take the previous one, square it, and add c to it. This generates an infinite series of complex numbers.

Something interesting happens with those numbers:

• For some starting c values, the numbers we generate will eventually escape the circle of radius 2 and go flying off to infinity, never to return.
• For other c values, the series of points will never leave the circle of radius 2 even under infinite iteration.

That last part is pretty weird! What would it look like if we showed all the starting points that never escape?

We’ve just found the Mandelbrot set.

Hold on, “infinite iteration?”

I used a bad word in that definition - computers don’t like the concept of infinity very much. I mean, they’re happy enough to do something forever, but we impatient humans aren’t very happy waiting around that long.

So, like the lazy programmers we are, we’ll pick a value for “infinity” and leave the theoretical perfection to the mathematicians. As it turns out, the value we pick changes the output considerably:

Here we have three renderings using values of 5, 10, and 15 as the maximum iteration limit. If the points are still within the circle after that many iterations, we assume they are in the Mandelbrot Set. As you can see, raising the limit gets us a more defined image.

For context…

To make it really concrete, the code to do the important bits we’ve covered so far is as follows:

public bool IsInMandelbrotSet(Complex c, int iterationLimit)
{
    var z = Complex.Zero;

    for (int i = 0; i < iterationLimit; i++)
    {
        z = z * z + c;

        // check if the point has escaped the circle of radius 2
        if (z.Magnitude * z.Magnitude > 4)
            return false;
    }

    return true;
}

Not too complicated. The only thing to keep in mind is that multiplication and addition with complex numbers is slightly more complicated than it appears. The check to see whether we’ve escaped the circle of radius 2 also looks scarier than it is - we’re just using the Pythagorean theorem.

Summary

So far we’ve been introduced to the Mandelbrot Set. In the next part we’ll start looking into how to visualize it, which will eventually bring us to the Buddhabrot.